classical-music | HamburgMusicNotation HMN

Download pdf-file

abschliessende-endfassung-schriftlich-munster23-05-24-englisch Download

Hamburg numerical music notation
Hamburg Music Notation (HMN)

Christian Pörksen and Harry Schreiber
Extended written version of a lecture from 29/10/22 at the
symposium Music and Brain in Münster

The English version of the publication was created with the help of the translation software Deepl http://www.deepl.com/translater.
Only a few manual corrections were necessary.
The original German version is the reference version.

Introduction:

Our topic is concerned with the question of whether it is possible to
capture well-tempered music in a mathematical number system in such a way
that it can be fully grasped and communicated in a way similar to the
binary or decimal number system.
We quote some thoughts that the brilliant researcher and thinker
Leibniz, who lived until 1715, thought and wrote down on the subject of
music (1) and please consider how long it took for his invention of the
binary number system (2), the basis of computer technology, to find its
way into our daily lives.
The introduction of the decimal system also met with considerable
resistance, especially in Germany, where, on the other hand, considerable
progress was made in mathematics and important open questions such as
Riemann’s conjecture were formulated (3).
All attempts to express music using a generally accepted number system
have failed so far and have met with fierce resistance from many
musicians. This is a serious problem that we also underestimated.
It is very easy to understand that the 12 tones of Western music can
also be named with a number or a letter or other symbols, for which
there is a list on the website
“The Music Notation Project Exploring Alternative Music Notation
Systems” provides numerous examples and graphical representations (4).
Our endeavours are also described in detail there or on our website (5).
We humans are almost all so used to calculating in the decimal system
that the introduction of the duodecimal system has not yet succeeded
despite all efforts. Many mathematicians, especially those of the
Dozenal Societies of the USA (6) and Great Britain (7), consider this
system to be more suitable than the decimal system.
Perhaps it will be possible to use music to establish the duodecimal
system alongside the decimal system and make music accessible and
understandable to all citizens as a basic element of human education –
as was already demanded in ancient Greece.
Like others, e.g. Tom Pendlebury (8), we try to explain in this article
why we consider the duodecimal number system suitable for closing
this gap.
Leibniz wrote about the importance of mathematics in music (1): “Music is
subordinate to arithmetic, and if you know some basic experiments with
harmonies and dissonances, you know that all other principles depend on
numbers”.
And quoted elsewhere, but from the same overview and not from the
original source:
“Because the intervals we use are all composed of ratios between the
prime numbers 1, 2, 3 and 5. If we were given a little more finesse, we
could also include those with the prime number 7″. And I believe that
this is indeed the case. That’s why the ancient world didn’t completely
shy away from the number seven. But there are hardly any people who also use the intervals of the nearest prime numbers 11 and 13.
I too have often thought about the question of what significance numbers,
and prime numbers in particular, have for music and have asked others
about this without finding a satisfactory answer.

Method:

In the following, we show that it is possible to fulfil all the
requirements of the Western notation system with the help of the
duodecimal system and simple graphical changes. Our own endeavours can be
found in detail under (9) and are briefly described here once again.
Two parameters of classical western music notation can be simplified.
1. To label the notes
It was an exhilarating moment when I realised one morning in my practice
room that there are only 12 notes in Western music, all of which can be
given a number name and written before all the accidentals, and I still
do this today, and it has made reading music in the usual treble clef
notation much easier for me, as the accidentals are no longer necessary.
At first I used the decimal system for labelling, but then I switched to
the duodecimal system, which can be used to represent all aspects of
well-tempered music and enables simple arithmetic operations within the
system, which is structured in “octaves”. It was then a long road to the
development of the duodecimal Hamburg Music Notation, which I called by
that name because I reject the common practice of using proper names and
because the name of the music city of Hamburg is memorable and was still
available at the time. The Hamburg Music Notation (HMN) can also be found
under the following names, all of which characterise important aspects of
this system: DCMN, Emojitype, Pianotype Notation, Hamburg Numerical Music
Notation.
2. To simplify the graphic
The typeface can and should also be simplified. You can find
our suggestions on the Internet. (5)
They are: Change as little as possible. No accidentals. No additional
clefs. The principle of black and white keys can be implemented using two
graphically distinguishable note heads (a) normal for notes on the white
keys and (b) cross as the note head for the black keys. The notes of all
octaves are shown in the same position on the lines and guides. We would
particularly like to draw your attention to our poster, which provides an
overview of all twelve major and minor keys and the most important chords
(10).
The poster shows you in the centre the new representation of the 12 keys
of Western music, expressed in 12 duodecimal digits and marked with six
colours on the 5 usual lines. Colour coding is not absolutely essential. For comparison, the 12 major and minor keys are
shown to the left and right in classical notation.
There are two software approaches. One comes from the company of my
Belgian partner Dominique Vandeneucker. Alternative Music Notation (11),
a numerical notation that can also be converted and written in Jianpu,
the numerical notation commonly used in Asia.
In co-operation with the programmer Robert Ipach, the free downloadable
beta version for Musescore (12) is now available, which can convert the
music notation from the usual to the Hamburg music notation with one
click. This version can only be used in Musescore 3.
Anyone interested in the subject can study numerous suggestions from
music enthusiasts at http://www.musicnotation.org (18).

Discussion:

We fully agree with the following quote:
“Bach’s compositional work “The Well-Tempered Clavier” (13), in which he
created scores for all 12 major and minor keys on the basis of
Werckmeister’s work (14) for the tuning of the piano with 12 keys, was a
great help for the further development of composition and music-making.
Bach treated all keys equally, according to the “compositional
principles” he had essentially developed on his own.
We have so many languages in the world and the lingua franca (15) of our
day is undoubtedly the English language.
Music is a universal language (16), but a lingua franca for music does
not exist – indeed, music has largely remained stuck at the level of
oral tradition in terms of its communication.
But a lingua franca for music is urgently needed, because without
definitions of the languages of music – its letters and its syntax – we
will never be able to communicate adequately.
In the Wikipedia article musical literacy (17) a figure of only around 9 per cent of the world’s population being able to read and write music is
mentioned. This article also discusses many aspects and new insights into
the reasons why music has largely remained stuck in the oral tradition.
On 29 October 2022, a conference on the subject of music and the brain
was held at the Physiological Institute of the University of
Münster under the direction of Erwin-Josef Speckmann and Klaus von Wild,
at which I was given the opportunity to present the music notation we
have developed under the title given above. The content of this
presentation forms the basis of this publication.
On my website (5) and on the pages of musicnotation.org (18) you will
find several descriptions of this by my co-author Harry Schreiber and
myself. These deal with the endeavours to make music easier to read and
have taken the endeavours of Read (19) as a basis for evaluation, even if
we do not agree with all the requirement criteria there. The chapter
Applications for the Duodecimal System of the Dozenal Society of Great Britain contains the article by Tom Pendlebury (20) and a reference to our representations:n”Hamburger Musik Notation, the description of a new notation for music by Christian Pörksen”:
Next to the clock, well-tempered music is probably the most common
practical application of the duodecimal principle currently in use.
Please download the pdf file with our ideas (21).
Firstly, we comment on the article on the homepage of the DSGB (“Dozenal Society of Great Britain”, title: Music á la Dozen, Chapter Applications, title: Music, Scales (20) Author: Tom Pendlebury, who deserves special mention here. This Englishman and dozenalist emphasised and justified the importance of the duodecimal system for music, but unfortunately died before he could complete his remarks. I was therefore no longer able to ask him why he labelled the first note of an octave(C) of the keyboard with zero and not with 1.
I am also grateful to the Dozenal Society of America (6) for the following statement in Vol. 05, Iss. 06:
In “The official newsletter of the Dozenal Society of America 1 September
1201″ (decimal converted 2017), Dr John Impagliazzo wrote: Music lovers
have long been interested in the duodecimal system; beginning with
Vodjevetz’s new music notation, the application of the duodecimal system
to music has been an ongoing concern. You may therefore be interested to
learn about Hamburg music notation:
Based on the observation that an “octave” consists of twelve semitones
and an “octave” comprises twelve semitones, notes are represented as
numerical values in Hamburg notation. Very interesting and worth a look
for those who are familiar with such things.
Dr John Impagliazzo has written extensively on well-tempered music and
scales in duodecimal notation (22).
Well-tempered music can be described mathematically using the duodecimal
position number system (23). This approach enables the development of
suitable software.
There is currently a beta version of an add-on for Musescore 3 available
for free download from Robert Ipach with our support (12), which enables
notes to be converted to HMN. The name of the notes in the text lines
below the note image can also be displayed.
Unfortunately, the music cannot yet be played after conversion, as
there are still some errors. Unfortunately, we currently lack the
financial resources to further improve and market the free software.
We are convinced that learning notation is much easier simply by labelling the notes with a number as a name. My teacher, solo trumpeter Boris Havkin (25), has had very good experiences with this in his many years of teaching beginners.
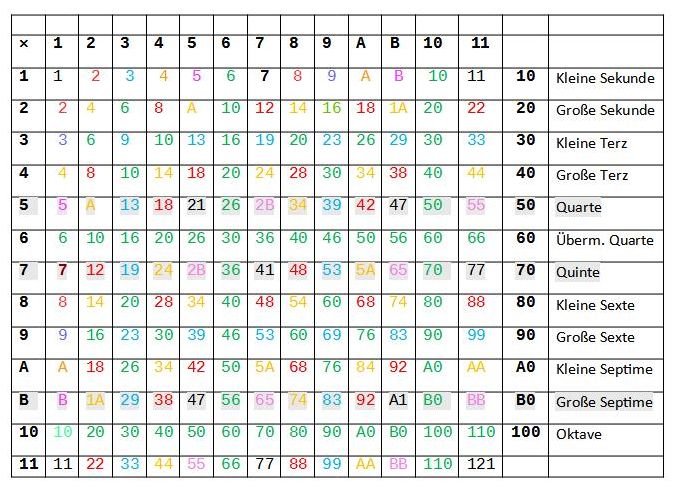
We have only slightly modified the duodecimal addition and multiplication table (Fig. 1) from 1-100 from Wikipedia in order to illustrate many aspects of music where the use of simple arithmetic operations are helpful.
Fig. 1 Duodecimal multiplication table

This means that not only the scales but also the circle of fourths,
circle of fifths and Bb circle (circle of elevenths) can be easily
mapped by addition and subtraction (Fig. 2). The term circle is
actually not a good term, as the notes are played upwards and downwards
and it would be better to think of a ladder that you can go up and down
or play. It is then possible to give each playable note a number that
clearly identifies it. However, such serious changes can only
be realized with a major international effort aimed at introducing the duodecimal system into twelve-tone music.
The structuring of the keyboard into blocks of 10 (decimal 12) keys
each results in a clear organisation. The prime number steps play a
special role here. The semitone steps are counted: The scale of fourths up and down follows +5 or-5 from each note. The scale of fifths up and down follows +7 or-7 from each note. The eleventh (Bb) scale up and down follows +B or -B from each note.
The system of chords (see Fig. 2) can also be easily represented and
learnt in the duodecimal system and could replace the current complex
system, which is only well mastered by a few. All aspects of Western
music can be represented mathematically. This also applies to all other
musical systems with equal temperament (24).

Fig.2 Prime number steps (5,7,B) are marked.
Duodecimal multiplication table modified for music

For the sake of clarity, this illustration does not include a translation of the German nomenclature.

We return to the starting point of our considerations and now essentially
limit ourselves to so-called Western music, whose development was
given such a decisive boost by the genius Johann Sebastian Bach with his
publication “The Well-Tempered Clavier” (13). We transferred Bach’s ideas
to the naming and position of the notes.
Wikipedia explains in detail why numbering systems make sense.
(23) Each of the twelve tones only needs one name to identify it.
Starting with C=1, the duodecimal system is used as
Positional numeral system used in the sequence 1,2,3,4,5,6,7,8,9,A,B,10.
Different symbols are used for ten and eleven in duodecimal notation; we
use A and B as in Wikipedia English, as in hexadecimal notation, so that
a duodecimal count from zero to twelve is 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A, B, 10.
The marking of the zero with a dot in the centre (0) in the duodecimal
system is a separate proposal and is available as a special character or
directly available in the Liberation Mono font.
In the following, we use both designations in parallel.
Decimal 1 2 3 4 5 6 7 8 9 10
Duodecimal 1 2 3 4 5 6 7 8 9 A B 10
We designate the decimal tenth position as A in duodecimal, the eleventh
as B and the duodecimal tenth as 10 and use a zero with a dot in the
centre to distinguish it from the decimal ten. Music is divided into
octaves, and the major and minor scales are the most commonly used
scales. These consist of eight notes.
It is important to note the following: the 8th note of a scale is also
the first note of the next higher scale. The connection is easier to
understand if we start from twelve-tone music. In this case, the octave
tone is already the 13th tone decimal and therefore the eleventh duodecimal tone.
After ten duodecimal multiplication steps or addition steps with the same
digit, we return to the starting number and the eleventh duodecimal tone
is therefore both the end point of the octave and the starting point
of the next higher octave.
Although the octave tone sounds similar to the original tone, it is a
completely new tone with different overtones and undertones and a
doubling of the original frequency. Each initial tone of an octave begins its own tonal world. If we transpose a composition into a different key, this measure can greatly change the sound.
Fig. 3 below shows you how each octave can be organised mathematically
using the note 5 (E) as an example. It is also suitable for practising all scales and chords for a specific pitch. Fig.(3) Exercise table for addition and subtraction shown in duodecimal:
Positions and range of the 10 ascending and descending intervals of all
scales using the example of tone 5=E as the base tone.
The prime number intervals are emphasised +/-5 semitones = (fourth), +/- 7 semitones = (fifth) and +/- B (dec.11) semitones.

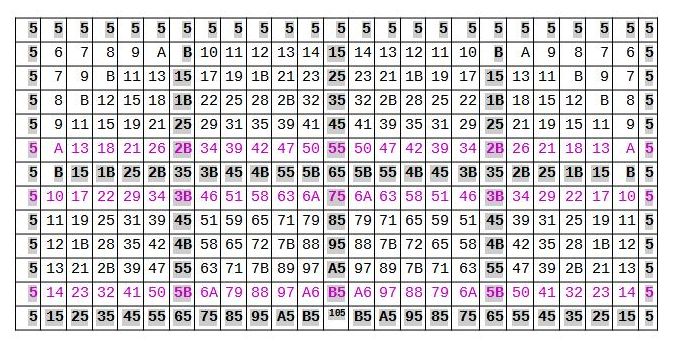
The circle of fourths, fifths and Bb can be read directly for each key
from the duodecimal addition table by adding the prime numbers 5, 7 and
B (11 decimal), and we recognise how the octaves can be divided into
ladders instead of circles, and that we should abandon the image of the
circle as an auxiliary number construction.
For the prime numbers 5, 7 and B (decimal 11), they repeat after every
10 (decimal 12) steps, and of course this also applies to every other
note. After 10 duodecimal steps, the next octave begins again with the
starting number on the scale-just one duodecimal step or one octave
higher.

Summary:

Human communication via sounds or complex music are probably the most frequently used languages of mankind. It is time to develop suitable, easy-to-learn written languages for them.

Only in this way can the prevailing musical illiteracy be eliminated and the full potential of this means of communication be realised.
When Martin Luther translated the Bible into German, the world changed
for many people. Something similar could happen if we humans could find
a lingua franca for music that is generally accepted.
We are convinced that the establishment of the duodecimal system in music by “well-tempering” the nomenclature of the notes can take over this task for the notes and that simple graphical solutions are possible by using two types of note heads based on the model of a conventional keyboard, as we have shown.
The vehicle of this simple musical written language could also be used to establish the duodecimal place value system as another basis of practical mathematics.

List of illustrations:

Fig.1 Duodecimal multiplication table
Fig.2 Duodecimal multiplication table modified for music

Fig.3 Octave-specific addition and multiplication table

Bibliography:

1) Leibniz,on the subject of music http://www.leibnizharmonien.de/

2)Binary number system https://de.wikipedia.org/wiki/Dualsystem#Entwicklung_des_Dualsystems

3) https://de.wikipedia.org/wiki/Riemannsche_Vermutung

4) https://musicnotation.org/wiki under Notation Systems

5) Hamburgmusicnotation.com

6) https://dozenal.org/

7 http://www.dozenalsociety.org.uk/

8) Search https://www.tapatalk.com/groups/dozensonline/discussion/all for Pendlebury

9) https://musicnotation.org/wiki/notation-systems/hamburg-music-notation-by-robert-elisabeth-key/

10) https://musicnotation.org/wiki/notation-systems/hmn-poster/