Skript Vortrag 29.10.2022

Download pdf-Datei

Click to access abschliessende-endfassung-schriftlich-munster-24-05-08.pdf

Übersicht Hamburg Musiknotation

Hamburger numerische Musiknotation

Hamburg Music Notation (HMN)

Christian Pörksen und Harry Schreiber

Erweiterte schriftliche Fassung eines Vortrags vom 29.10.22

auf dem Symposium Musik und Gehirn in Münster

Einleitung:

Unser Thema befasst sich mit der Frage, ob es gelingen kann, die wohltemperierte Musik so in ein mathematisches Zahlensystem zu fassen, dass sie komplett erfasst werden kann und ähnlich gut vermittelt werden kann wie das binäre oder dezimale Zahlensystem.

Wir zitieren einige Gedanken, die der geniale Forscher und Denker Leibniz, der bis 1715 lebte,zum Thema Musik (1) gedacht und aufgeschrieben hat und bedenken Sie alle bitte dabei, wie lange es dauerte, bis seine Erfindung des binären Zahlensystems (2) als Grundlage der Computertechnik in unser aller Leben tagtäglich Eingang fand.

Auch die Einführung des Dezimalsystems stieß auf erheblichen Widerstand, besonders in Deutschland, wo andererseits erhebliche Fortschritte für die Mathematik entstanden und auch bedeutende offene Fragen wie die Riemannsche Vermutung formuliert wurden (3).

Alle Versuche, die Musik mit einem allgemein akzeptierten Zahlensystem auszudrücken, sind bisher gescheitert und stoßen bei vielen Musikern auf erbitterten Widerstand. Hier liegt ein auch von uns unterschätztes schwerwiegendes Problem.

Es ist zwar sehr einfach zu verstehen, dass man die 12 Töne der westlichen Musik auch mit einer Zahl oder einem Buchstaben oder anderen Symbolen benennen kann, wofür es auf der Internetseite „The Musicnotation Project Exploring Alternative Music Notation Systems“ zahlreiche Beispiele und grafische Darstellungen gibt (4).

Auch unsere Bemühungen sind dort oder auf unserer Internetseite ausführlich dargestellt (5).

Wir Menschen sind fast alle das Rechnen im Dezimalsystem so gewohnt, dass die Einführung des Duodezimalsystems bisher trotz aller Bemühungen nicht gelungen ist. Viele Mathematiker, insbesondere die der Dozenal Societies der USA (6) und Großbritanniens (7), halten dieses System für geeigneter als das Dezimalsystem.

Vielleicht gelingt es ja über die Musik, das Duodezimalsystem neben dem Dezimalsystem zu etablieren und darüber die Musik als Grundelement menschlicher Bildung – wie schon im antiken Griechenland gefordert – für alle Bürger zugänglich und verstehbar zu machen.

Wie andere, z.B. Tom Pendlebury (8), versuchen auch wir in diesem Artikel zu erläutern, warum wir das duodezimale Zahlensystem für geeignet halten, diese Lücke zu schließen.

Leibniz schrieb zur Bedeutung der Mathematik in der Musik (1): „Die Musik ist der Arithmetik untergeordnet, und wenn man einige grundlegende Versuche mit Harmonien und Dissonanzen kennt, weiß man, dass alle übrigen Prinzipien von Zahlen abhängen“.

Und an anderer Stelle, aber aus der gleichen Übersicht und nicht aus der Originalquelle zitiert: „Denn die von uns benutzten Intervalle sind alle aus Verhältnissen zwischen den Primzahlen 1, 2, 3 und 5 zusammengesetzt. Wenn uns etwas mehr Feinheit gegeben wäre, könnten wir auch die mit der Primzahl 7 einbeziehen. Und ich glaube, dass es das in der Tat gibt. Deshalb hat die Antike die Zahl sieben nicht völlig gescheut.“

Aber es wird kaum Menschen geben, die auch die Intervalle aus den nächsten Primzahlen 11 und 13 verwenden.

Gedanklich habe auch ich mich oft mit der Frage beschäftigt, welche Bedeutung mögen Zahlen und insbesondere Primzahlen für die Musik haben und habe andere dazu befragt, ohne darauf eine mich befriedigende Antwort zu bekommen.

Methode:

Im folgenden stellen wir dar, dass es gelingen kann, mit Hilfe des Duodezimalsystems und einfacher grafischer Änderungen alle Anforderungen, die das westliche Notensystem stellt, zu erfüllen. Unsere eigenen Bemühungen finden sie detailliert unter (9) und werden hier noch einmal kurz dargestellt. Zwei Parameter der klassischen westlichen Musiknotation können vereinfacht werden. 1. Zur Bezeichnung der Noten

Es war ein beglückender Moment, als mir eines Morgens in meinem Übungskeller klar wurde: es gibt in der westlichen Musik nur 12 Töne, die man alle mit einem Zahlennamen versehen und vor alle Vorzeichennoten schreiben kann, und das praktiziere ich bis heute, und es hat das Lesen von Musik in der üblichen Notation im Violinschlüssel für mich sehr vereinfacht, da die Vorzeichen entfallen. Zunächst habe ich das Dezimalsystem zur Kennzeichnung benutzt und bin dann aber auf das duodezimale System übergegangen, mit dem alle Aspekte der wohltemperierten Musik dargestellt werden können und das einfache Rechenoperationen innerhalb des in „Oktaven“ aufgebauten Systems ermöglicht. Es war dann ein langer Weg zur Entwicklung der duodezimalen Hamburger Musik Notation, die ich so nannte, weil ich die vielfach geübte Bezeichnung mit Eigennamen ablehne und weil der Name der Musikstadt Hamburg einprägsam ist und damals dafür noch frei war. Die Hamburger Musik Notation (HMN) ist auch auch unter folgenden Bezeichnungen zu finden, die alle wichtige Aspekte dieses Systems kennzeichnen: DCMN, Emojitype, Pianotype Notation, Hamburger numerische Musiknotation.

2. Zur Vereinfachung der Grafik Auch das Schriftbild kann und sollte vereinfacht werden. Unsere Vorschläge dazu finden sie im Internet. (5) Sie lauten: Möglichst wenig verändern. Keine Vorzeichen. Keine zusätzlichen Notenschlüssel. Das Prinzip der schwarzen und weißen Tasten lässt sich durch zwei grafisch unterscheidbare Notenköpfe (a) normal für Noten der weißen Tasten und (b) Kreuz als Notenkopf für die schwarzen Tasten umsetzen. Die Noten aller Oktaven sind an der jeweils gleichen Position auf den Linien und Hilfslinien dargestellt. Besonders hinweisen möchten wir auf unser Poster, das alle zwölf Tonarten in Dur und Moll und die wichtigsten Akkorde in einer Übersicht darstellt (10). Das Poster zeigt Ihnen in der Mitte die neue Darstellung der 12 Tonarten der westlichen Musik in 12 Ziffern duodezimal ausgedrückt und mit sechs Farben markiert auf den 5 üblichen Linien. Eine Farbmarkierung ist nicht zwingend erforderlich. Zum Vergleich sind links und rechts daneben die 12 Tonarten in Dur und Moll in der klassischen Notation dargestellt.

Es liegen zwei Softwareansätze vor. Der eine stammt von der Firma meines belgischen Partners Dominique Vandeneucker. Alternative Music Notation (11), eine Ziffernnotation, welche auch in die in Asien gebräuchliche Ziffernnotation Jianpu umgewandelt und geschrieben werden kann. In Zusammenarbeit mit dem Programmierer Robert Ipach liegt inzwischen die frei downloadfähige beta Version für Musescore (12) vor, die das Notenbild mit einem Klick von der üblichen in die Hamburger Musiknotation umwandeln kann. Diese Version kann nur in Musescore 3 genutzt werden. Wer sich für das Thema interessiert, kann dazu zahlreiche Vorschläge von der Musik begeisterter Menschen auf http://www.musicnotation.org (18) studieren.

Diskussion:

Mit folgendem Zitat stimmen wir voll überein: „Eine große Hilfe für die Fortentwicklung des Komponierens und Musizierens war Bachs kompositorisches Werk „Das wohltemperierte Klavier“ (13), in dem er für alle 12 Dur- und Moll-Tonarten Partituren erschuf auf den Grundlagen von Werckmeister’s Arbeiten (14) für die Stimmung des Klaviers mit 12 Tasten. Alle Tonarten wurden von Bach darin gleichwertig behandelt, nach den von ihm im wesentlichen autodidaktisch entwickelten kompositorischen Prinzipien“. Wir haben so viele Sprachen auf der Welt und die Lingua franca (15) unserer Tage ist zweifellos die englische Sprache. Musik ist eine universelle Sprache (16), aber eine Lingua franca für die Musik existiert nicht – ja, die Musik ist bezüglich ihrer Vermittlung weitgehend auf dem Stand der mündlichen Tradition steckengeblieben. Doch eine Lingua franca für die Musik ist dringend erwünscht, denn ohne Definitionen der Sprachen der Musik – ihrer Buchstaben und ihrer Syntax – werden wir uns nie hinreichend verständigen können. In dem Wikipedia Artikel musical literacy (17) – im Deutschen fehlt dafür leider ein so passender Begriff – wird eine Zahl von etwa nur 9 Prozent der Weltbevölkerung genannt, die Musik lesen und schreiben kann. In diesem Artikel werden auch viele Aspekte und neue Erkenntnisse zu den Ursachen erörtert, weshalb die Musik weitgehend in der mündlichen Tradierung steckengeblieben ist. Am 29.10.2022 fand in den Räumen des Physiologischen Instituts der Universität Münster unter der Leitung von Erwin-Josef Speckmann und Klaus von Wild eine Tagung statt zum Thema Musik und Gehirn, auf der mir die Gelegenheit gegeben wurde, die von uns entwickelte Musiknotation unter dem oben angegebenen Titel darzustellen. Der Inhalt dieses Vortrags bildet die Grundlage dieser Publikation. Auf meiner Website (5) und auf den Seiten von musicnotation.org (18) finden sich dazu mehrere Darstellungen von meinem Coautor Harry Schreiber und mir. Diese befassen sich mit den Bestrebungen, Musik einfacher lesbar zu machen und haben sich die Bestrebungen von Read (19) als Grundlage zur Beurteilung zum Vorbild genommen, wenn wir auch nicht mit allen dortigen Anforderungskriterien übereinstimmen. Im Kapitel Applications für das Duodezimalsystem der Dozenal Society of Great Britain findet sich der Artikel von Tom Pendlebury (20) und ein Hinweis auf unsere Darstellungen: „Hamburger Musik Notation, die Beschreibung einer neuen Notation für Musik von Christian Pörksen“: Wohltemperierte Musik ist wahrscheinlich neben der Uhr die häufigste praktische Anwendung des Duodezimalprinzips, die derzeit verwendet wird. Bitte laden Sie die pdf-Datei mit unseren Ideen herunter (21). Zunächst kommentieren wir den Artikel auf der Homepage der DSGB (Dozenal Society of Great Britain“,Titel: Music á la Dozen, Kapitel Anwendungen, Titel: Musik, Tonleitern (20) Autor: Tom Pendlebury,der hier besonders hervorgehoben werden muss. Dieser Engländer und Dozenalist hat die Bedeutung des Duodezimalsystems für die Musik hervorgehoben und begründet, starb aber leider, bevor er seine Ausführungen vollenden konnte. Daher konnte ich ihn nicht mehr fragen, warum er den ersten Ton einer Oktave (C) der Klaviatur mit Null und nicht mit der 1 kennzeichnete. Auch der Dozenal Society of America (6) bin ich dankbar für folgende Stellungnahme im Vol. 05, Iss. 06: Im Magazin „The official newsletter of the Dozenal Society of America 1. September 1201“ (dezimal umgerechnet 2017) schrieb Dr.John Impagliazzo (Übersetzung aus dem Englischen): Musikliebhaber interessieren sich schon lange für das Duodezimalsystem; beginnend mit Vodjevetz’ neuer Musiknotation, war die Anwendung des Duodezimalsystems auf die Musik ein ständiges Anliegen. Deshalb ist es für Sie vielleicht interessant, etwas über die Hamburger Musik Notation zu erfahren:
Ausgehend von der Beobachtung, dass eine “Oktave” aus zwölf Halbtönen besteht und eine “Oktave” zwölf Halbtöne umfasst, werden in der Hamburger Notation die Noten als numerische Größen dargestellt. Sehr interessant und einen Blick wert für diejenigen, die sich mit solchen Dingen auskennen. Dr.John Impagliazzo hat sich ausführlich mit wohltemperierter Musik und Tonleitern in duodezimaler Darstellung beschäftigt (22).

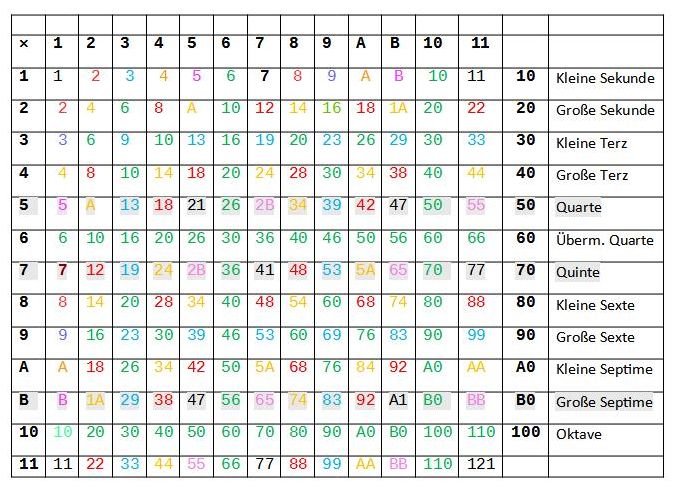
Die wohltemperierte Musik lässt sich mathematisch durch das duodezimale Positionszahlensystem (23) beschreiben. Dieses Vorgehen ermöglicht die Entwicklung geeigneter Software. Derzeit liegt ein von Robert Ipach mit unserer Unterstützung frei downloadbares Addon zu Musescore 3 in einer Betaversion vor (12), das eine Umwandlung von Noten in die HMN ermöglicht. Auch der Name der Noten in den Textzeilen unterhalb des Notenbildes kann angezeigt werden. Leider kann die Musik nach Umwandlung noch nicht abgespielt werden, da noch einige Fehler vorliegen. Für eine weitere Vervollkommnung und Vermarktung der freien Software fehlen uns derzeit leider die finanziellen Mittel. Wir sind überzeugt davon, dass das Erlernen der Notation allein durch die Bezifferung der Noten mit einer Zahl als Namen vieles vereinfacht. Mein Lehrer, der Solotrompeter Boris Havkin (25), hat damit in seinem langjährigen täglichen Unterricht von Anfängern sehr gute Erfahrungen gemacht. Die duodezimale Additions- und Multiplikationstabelle (Abb. 1) von 1-100 aus Wikipedia haben wir nur leicht verändert, um viele Aspekte der Musik darzustellen bei denen die Anwendung von einfachen Rechenoperationen hilfreich ist.

Abb. 1 Duodezimale Multiplikationstabelle

So lassen sich nicht nur die Tonleitern sondern auch Quartenzirkel, Quintenzirkel und B-Zirkel (Elfer-Zirkel) durch Addition und Subtraktion einfach abbilden (Abb. 2). Der Begriff Zirkel ist eigentlich kein guter Begriff, da die Töne aufwärts und abwärts gespielt werden und es besser wäre, von einer Leiter auszugehen, die man auf und ab gehen bzw. spielen kann. Es ist dann möglich, jeden spielbaren Ton mit einer Ziffer zu versehen, die diesen eindeutig identifiziert. Solche gravierenden Änderungen lassen sich aber nur mit großer internationaler Anstrengung umsetzen, welche die Einführung des Duodezimalsystems in der zwölfstufigen Musik zum Ziel hat. Die Strukturierung der Klaviatur in Blöcke von jeweils 10 (dezimal 12) Tasten ergibt eine klare Gliederung. Dabei spielen die Primzahlstufen eine besondere Rolle. Gezählt werden die Halbtonschritte: Die Quartenleiter aufwärts und abwärts folgt +5 oder-5 von jedem Ton aus. Die Quintenleiter aufwärts und abwärts folgt +7 oder-7 von jedem Ton aus. Die Elfer(B)-Leiter aufwärts und abwärts folgt +B oder –B von jedem Ton aus. Auch die Systematik von Akkorden (s. Abb 2) lässt sich im Duodezimalsystem einfach darstellen und erlernen und könnte das gegenwärtige komplexe System ablösen, welches nur von wenigen gut beherrscht wird. Alle Aspekte der westlichen Musik lassen sich mathematisch abbilden. Dieses gilt auch für alle anderen Musiksysteme mit gleichstufiger Stimmung (24).

Abb.2 Primzahlstufen (5,7,B) sind markiert. Duodezimale Multiplikationstabelle modifiziert für die Musik

Wir kehren zum Ausgangspunkt unserer Betrachtungen zurück und beschränken uns jetzt im wesentlichen auf die sogenannte westliche Musik, deren Entwicklung der geniale Johann-Sebastian Bach einen so entscheidenden Entwicklungsschub gab mit seiner Publikation „Das Wohltemperierte Klavier“ (13). Wir übertrugen Bachs Gedanken auf die Benennung und Position der Töne. Warum Positionszahlensysteme sinnvoll sind, wird in Wikipedia ausführlich erklärt (23): Jeder der zwölf Töne braucht nur einen Namen zu seiner Identifizierung.

Beginnend mit C=1 wird das Duodezimalsystem als Positionszahlensystem in der Reihung 1,2,3,4,5,6,7,8,9,A,B,10 benutzt. Für zehn und elf in der Duodezimaldarstellung werden verschiedene Symbole verwendet; wir benutzen wie in Wikipedia-englisch A und B, wie in der Hexadezimaldarstellung, so dass eine Duodezimalzählung von null bis zwölf 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10 lautet.

Die Kennzeichnung der Null mit einem Punkt in der Mitte (0) im Duodezimalsystem ist ein eigener Vorschlag und ist als Sonderzeichen verfügbar oder direkt verfügbar in der Schrifttype Liberation Mono.

Wir benutzen im folgenden beide Bezeichnungen parallel.

Dezimal 1 2 3 4 5 6 7 8 9 10

Duodezimal 1 2 3 4 5 6 7 8 9 A B 10

Die dezimal zehnte Position bezeichnen wir duodezimal mit A, die elfte mit B und die duodezimal zehnte mit 10 und benutzen eine Null mit einem Punkt in der Mitte als Zeichen der Unterscheidung von der dezimalen Zehn.

Die Musik wird in Oktaven gegliedert, und als Tonleitern werden die Dur-Tonleitern und Moll-Tonleitern am häufigsten angewandt. Diese bestehen aus acht Tönen.

Dabei ist folgender Sachverhalt wichtig zu beachten: der 8. Ton einer Tonleiter ist bereits auch der erste Ton der nächsthöheren Tonleiter.

Der Zusammenhang ist einfacher zu verstehen, wenn wir von der Zwölftonmusik ausgehen. Dann ist nämlich der Oktavton bereits der 13.Ton und somit der elfte duodezimale Ton.

Nach zehn duodezimalen Multiplikationsschritten oder Additionsschritten mit der gleichen Ziffer kommen wir wieder auf die Ausgangszahl und der elfte duodezimale Ton ist somit zugleich Endpunkt der Oktave und gleichzeitig Ausgangspunkt der nächsthöheren Oktave.

Der Oktavton klingt zwar ähnlich wie der Ausgangston, ist aber doch ein völlig neuer Ton mit anderen Ober- und Untertönen und einer Verdoppelung der Ausgangsfrequenz. Mit jedem Ausgangston einer Oktave beginnt eine eigene Tonwelt.

Transponieren wir eine Komposition in eine andere Tonart, so kann diese Maßnahme das Klangbild stark verändern.

Die folgende Abb. 3 zeigt Ihnen am Beispiel des Tons 5 (E), wie sich jede Oktave mathematisch gliedern lässt. Sie eignet sich auch zum Üben aller Tonleitern und Akkorde für eine bestimmte Tonhöhe.

Abb. (3) Übungstabelle für Addition und Subtraktion

Duodezimal dargestellt:

Positionen und Tonumfang der 10 auf- und absteigenden Intervalle aller Tonleitern am Beispiel von Ton 5=E als Basiston

Hervorgehoben die Primzahlintervalle

+/-5 Halbtöne = (Quarte), +/- 7 Halbtöne = (Quinte) und +/- B (dez.11) Halbtöne

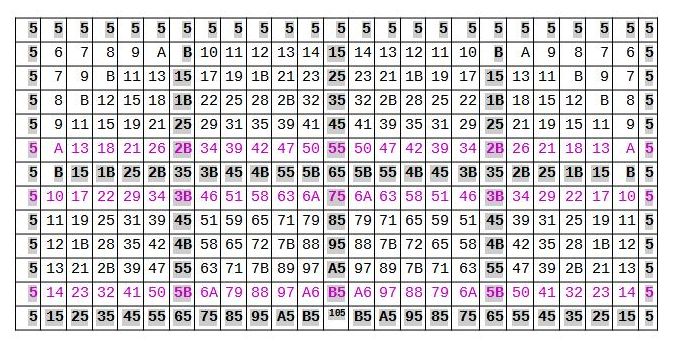
Der Quarten- , Quinten- und der B-zirkel lassen sich für jede Tonart direkt ablesen aus der duodezimalen Additionstabelle durch Addition der Primzahlen 5, 7 und B (11 dezimal), und wir erkennen, wie sich die Oktaven gliedern lassen in Leitern statt Zirkeln, und dass wir das Bild des Kreises als Hilfszahlenkonstruktion verlassen sollten.

Für die Primzahlen 5,7 und B (dezimal 11) gilt, dass sie sich nach jeweils 10 (dezimal 12) Schritten wiederholen, und dieses gilt natürlich auch für jeden anderen Ton. Nach 10 duodezimalen Schritten beginnt die nächste Oktave wieder mit der Ausgangszahl auf der Tonleiter – halt einen duodezimalen Schritt oder eine Oktave höher.

Zusammenfassung:

Zwischenmenschliche Verständigung über Töne oder komplexe Musik sind
wohl die am häufigsten benutzten Sprachen der Menschheit.
Es ist an der Zeit, für sie geeignete leicht erlernbare Schriftsprachen
zu entwickeln. Nur so kann der bisher vorherrschende musikalische
Analphabetismus beseitigt werden und sich das volle Potenzial dieser Verständigungsmöglichkeit entfalten.
Als Martin Luther die Bibel ins Deutsche übersetzte, veränderte sich für
viele Menschen die Welt. Ähnliches könnte geschehen, wenn wir Menschen eine Lingua franca, die allgemein akzeptiert wird, für die Musik finden. Wir sind davon überzeugt, dass die Etablierung des Duodezimalsystems in
der Musik diese Aufgabe durch “Wohltemperierung” der Nomenklatur für
die Töne übernehmen kann, und dass einfache grafische Lösungen durch Verwendung von zwei Notenkopftypen nach dem Vorbild einer Klaviatur, wie von uns aufgezeigt, möglich sind.
Über das Vehikel dieser einfachen musikalischen Schriftsprache könnte
sich auch das duodezimale Positionszahlensystem als eine weitere Grundlage praktischer Mathematik etablieren.

Abbildungsverzeichnis:

Abb.1 Duodezimale Multiplikationstabelle

Abb.2 Duodezimale Multiplikationstabelle modifiziert für die Musik

Abb.3 Oktavenspezifische Additions- und Multiplikationstabelle

Literaturverzeichnis:

1) Leibniz,zum Thema Musik http://www.leibnizharmonien.de/

2) binäres Zahlensystem https://de.wikipedia.org/wiki/Dualsystem#Entwicklung_des_Dualsystems

3) https://de.wikipedia.org/wiki/Riemannsche_Vermutung

4) https://musicnotation.org/wiki unter Notation Systems

5) Hamburgmusicnotation.com

6) https://dozenal.org/

7 http://www.dozenalsociety.org.uk/